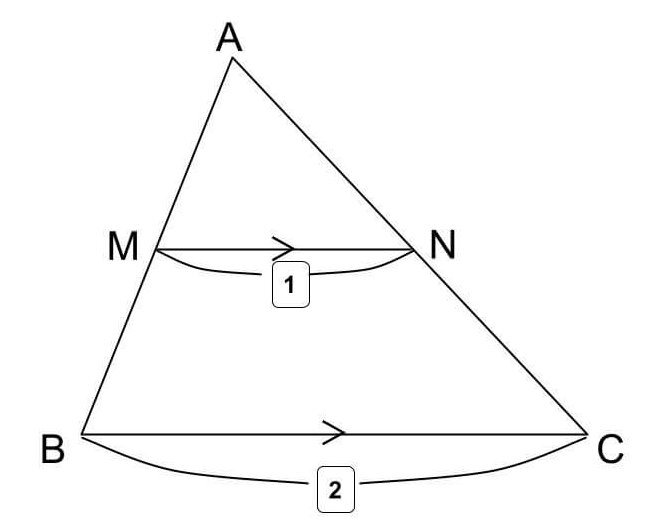
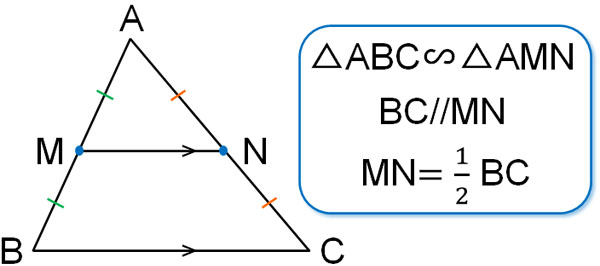
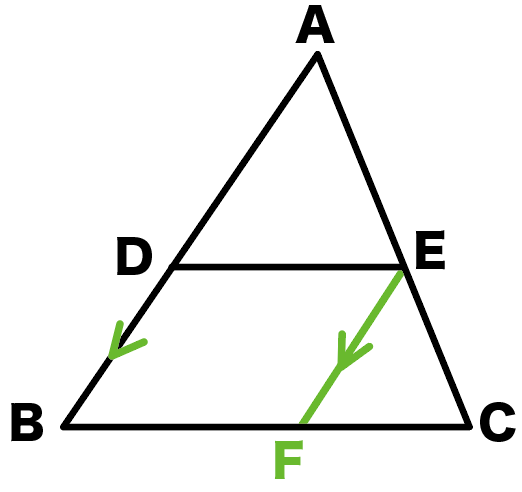
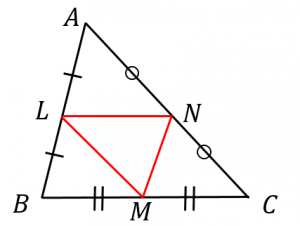
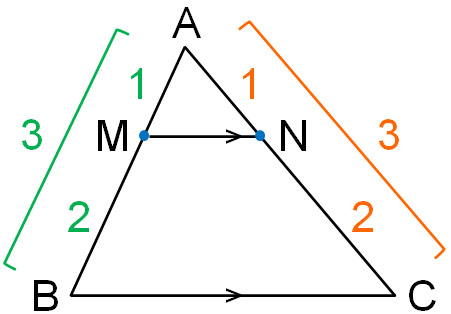
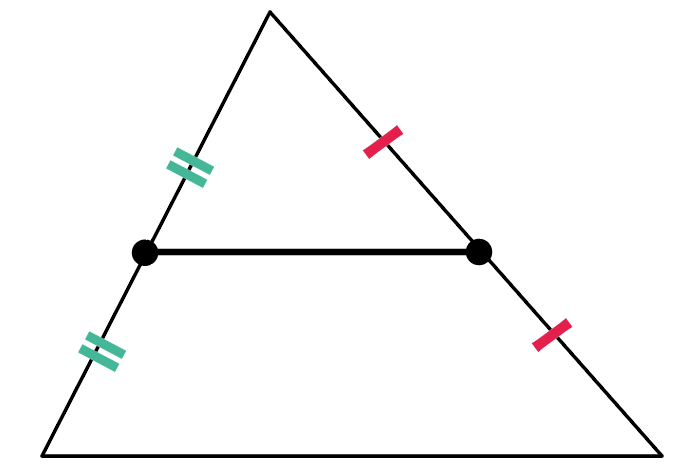
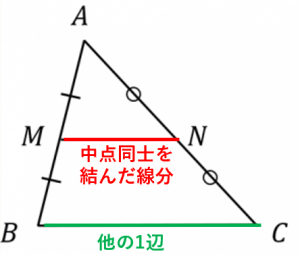
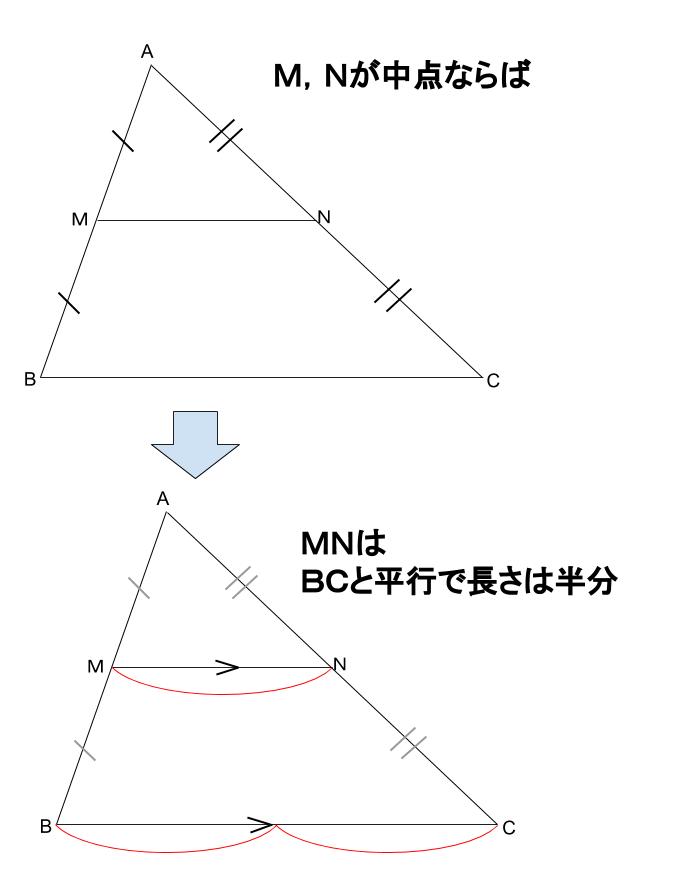
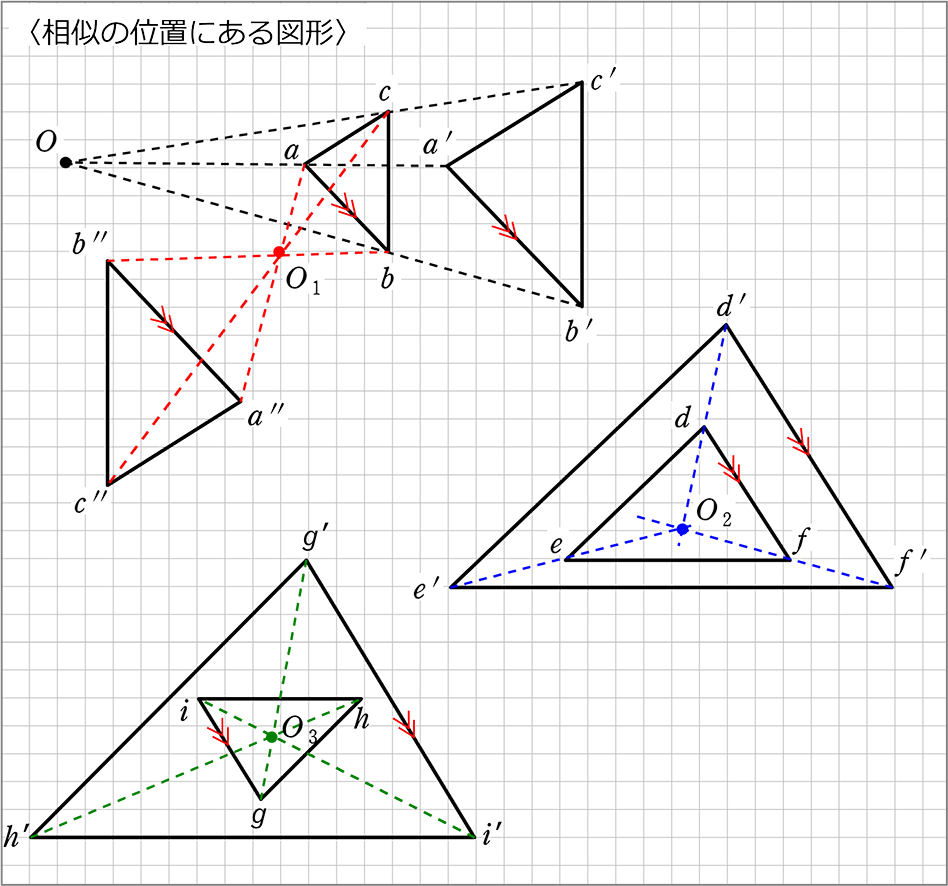
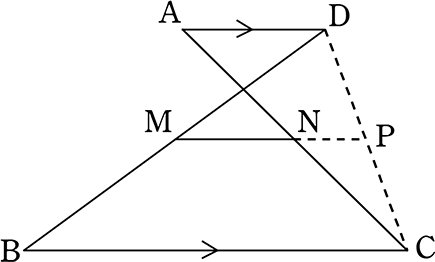
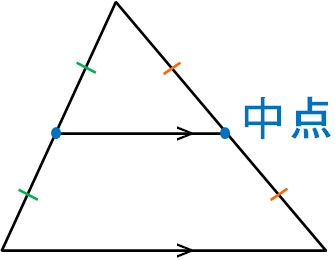
Web定理 三角形の底辺を除く2 辺のそれぞれの中点を結んだ線分「中点連結」は、底辺と平行であり、長さは底辺の半分に等しい 。 また、相似比が12の相似な三角形ができる 。 証明 以下に
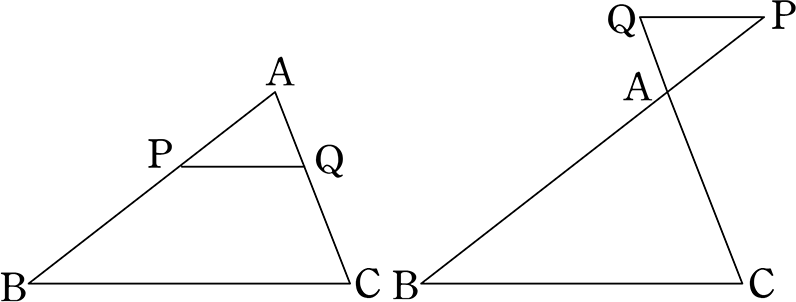
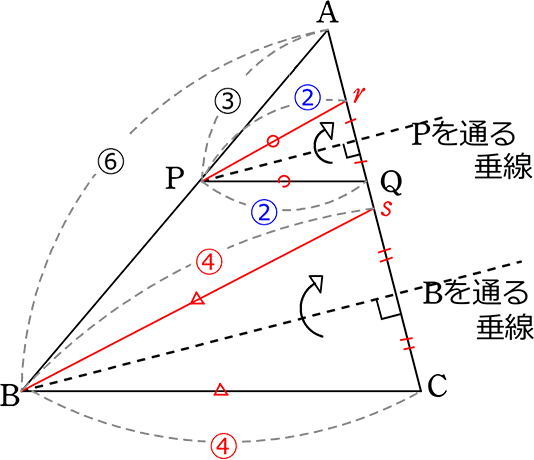
三角形と比の定理の逆 証明-Webよって apqr=aqqc ③ 次に四角形pbrqは平行四辺形なので、 pb=qr ④ ③と④より、 apqr=aqqc=appb=aqqc 以上で定理が成り立つことが証明できた。 証明おわり。 平行線とWeb 中点連結定理とは?証明、定理の逆や応用、問題の解き方 受験辞典 三角形の中点連結は、底辺と平行の方向を持つ。 b 三角形の中点連結は、底辺の半分の長さを持つ。
三角形と比の定理の逆 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 |  |  |
「三角形と比の定理の逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 | ||
「三角形と比の定理の逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
 |  |  |
「三角形と比の定理の逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「三角形と比の定理の逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | 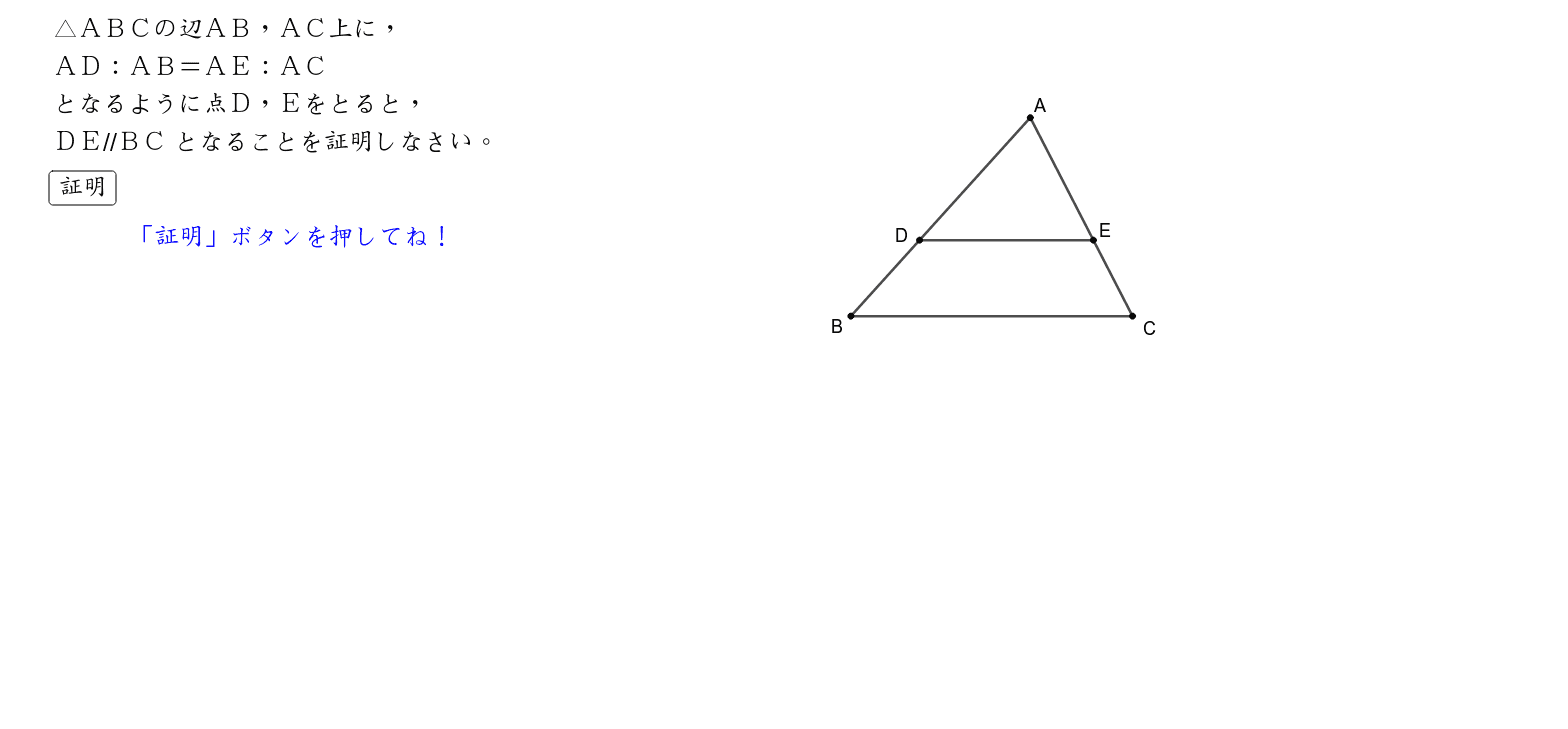 |
 | ||
 |  |  |
「三角形と比の定理の逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
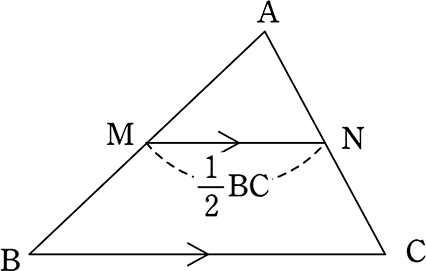 |  |  |
「三角形と比の定理の逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「三角形と比の定理の逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「三角形と比の定理の逆 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
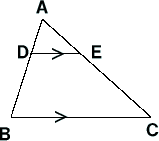
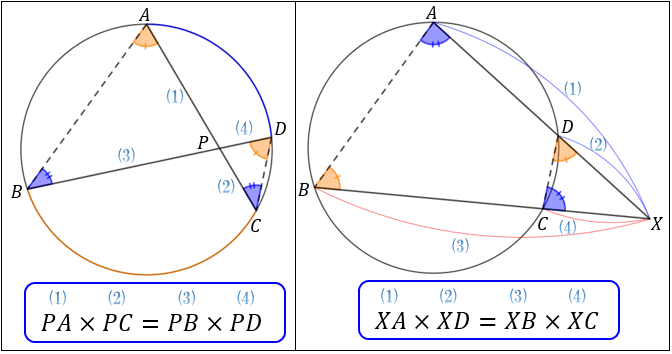
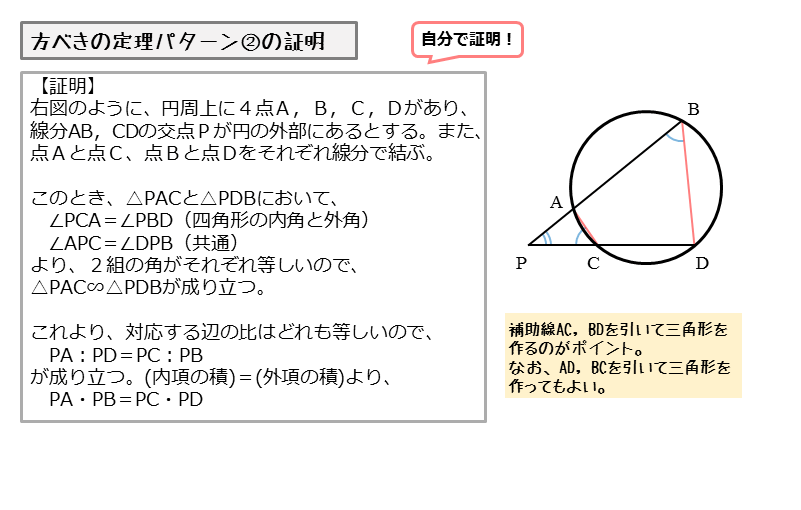
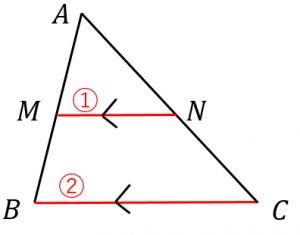
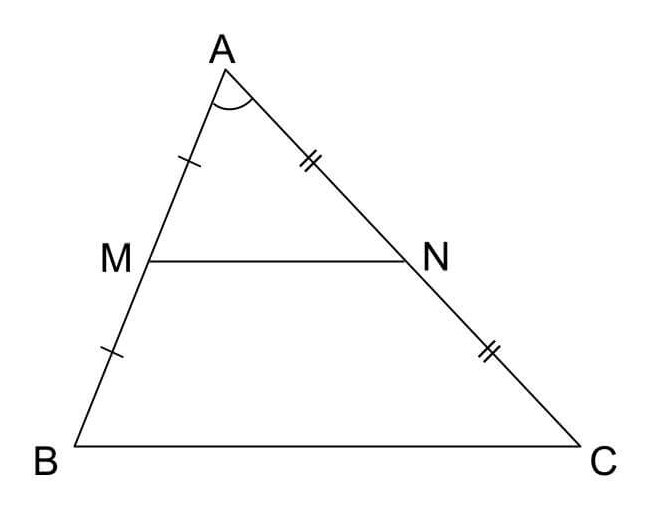
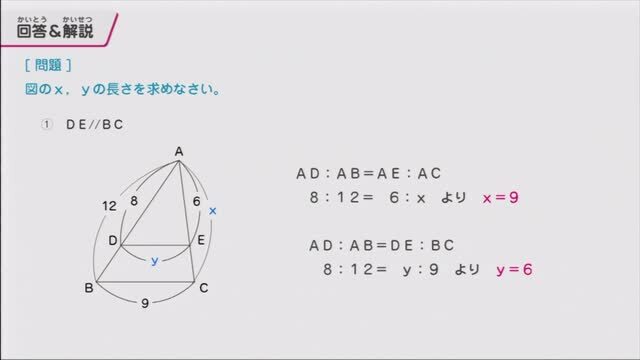
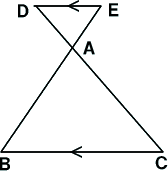
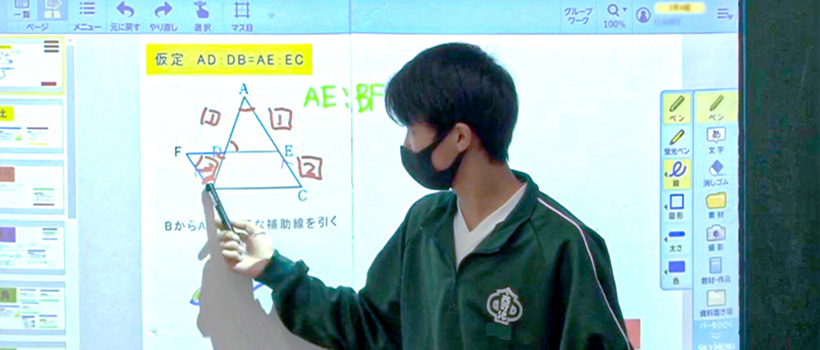
Web余弦定理(よげんていり、英 law of cosines, cosine formula )とは、平面上の三角法において三角形の辺の長さと内角の余弦の間に成り立つ関係を与える定理である 。 余弦定理を証明Web1.三角形と比の定理の逆を次のように証明した。空欄をうめなさい。 a <仮定> ad:db=ae:ec <結論> de//bc
Incoming Term: 三角形と比の定理の逆 証明,




0 件のコメント:
コメントを投稿